Disclaimer: Dieser Thread wurde aus dem alten Forum importiert. Daher werden eventuell nicht alle Formatierungen richtig angezeigt. Der ursprüngliche Thread beginnt im zweiten Post dieses Threads.
Logistische Regression
Hallo beinander,
Ich lerne gerade auf PR und hänge gerade bei Logistischer Regression. Die Folien gibt’s hier
Ich habe etwas in Octave rumgespielt und zu meinen Ergebnissen ein paar Fragen:
- Frage:
Wie kann ich in octave anständig die Legende plotten?
Hab die nun in GIMP nachbearbeitet…
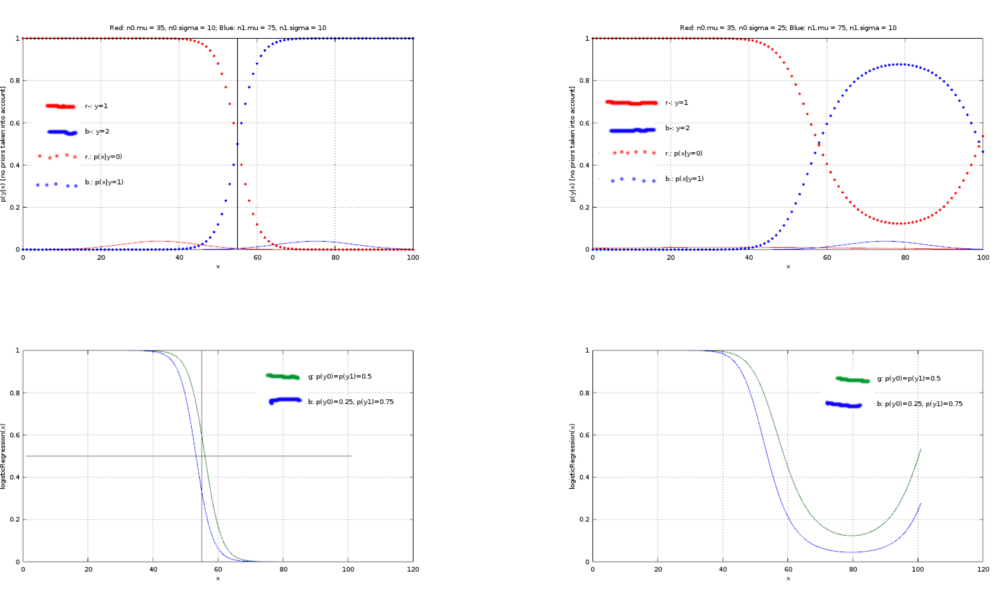
Okay, was man hier sieht:
In den oberen beiden Plots sieht man mit den durchgezogenen Linien je zwei Gaussfunktionen:
- N1(mu=35,sigma=10)
- N2(mu=75,simga=10)
Gepunktet ist die Wahrscheinlichkeit für die Klasse y eingezeichnet. Habe ich folgendermaßen berechnet: p(y=0|x) = p(x|y=0) / [ p(x|y=0) + p(x|y=1) ]
Umgangssprachlich ausgedrückt: Die Wahrscheinlichkeit für Klasse y=0 an der Stelle x, ist der Wert von y=0 an der Stelle x dividiert durch die Summe der beiden Funktionen an x.
In den beiden unteren Plots sieht man die logistische Funktion für y=0, mit unterschiedlichen prior-Wahrscheinlichkeiten.
- Frage:
Für die priori-Wahrscheinlichkeiten p(y=0)=p(y=1)=0.5 (links unten, grüner Plot) müssten die resultierende posteriori-Wahrscheinlichkeit zum Einen
- gleich der Wahrscheinlichkeit sein, die im oberen Plot Rot-gepunktet eingezeichnet ist, oder? Und zum Anderen
- (mMn) p=0.5 genau zwischen den beiden Gaussfunktionen haben, da beide Funktionen die gleiche Varianz haben. Also bei (mu1 + mu2)/2 = (35+75)/2 = 55. Das schwarz eingezeichnete Kreuz markiert diesen Punkt, der grüne Graph geht aber nicht durch. Warum?
- Frage:
Rechts ist die Varianz der Roten Funktion mit sigma=25 höher.
- N1(mu=35,sigma=25)
- N2(mu=75,simga=10)
Dadurch wird die Funktion flacher, aber auch deutlich breiter. So breit, dass sie sogar für große x irgendwann wieder über dem blauen Graph liegt.
Dadurch nimmt die gepunktete Rote Linie auch irgendwann wieder zu, bzw. die gepunktete blaue Linie ab. Macht Sinn.
Warum nimmt aber auch die Logistische Funktion wieder zu? Sollte die Logistische Funktion nicht streng monoton steigend (fallend) sein?
-
Frage:
Dass, wie eben beschrieben, die Rote Gausskurve für große x wieder über der Blauen Gausskurve ist, ist auch eine Erklärung, warum auf Folie 17 die Hyperbel plötzlich wieder oben rechts im Plot erscheint, oder? -
Frage:
In den Folien sind in den 2D-Plots unterschiedliche priori-Wahrscheinlichkeiten durch unterschiedliche Dichte der Punktwolken dargestellt. Wie könnte man das hier bei meinen 1D Plots ausdrücken?
Wäre es legitim die Höhe der Plots anzupassen? Also bei einer Gaussfunktion:

Den Vorfaktor 1/(sigmasqrt(2pi)) anzupassen?
Dadurch wäre dann natürlich die Fläche unter der Kurve nichtmehr 1, aber es würde relativ zur Fläche der anderen Funktion ja ausdrücken wie ausschlaggebend sie ist.
Danke für Antworten und Hilfe!
Hier noch der Vollständigkeit halber der Octave-Code, highlighten geht für Octave/Matlab im Forum nicht, oder?
clear all;
close all;
%Parameters of Gaussian for class y=0
n0.mu = 35; %mean
n0.sigma = 10; % deviation
py0 = 0.5; % prior-probability
%Parameters of Gaussian for class y=1
n1.mu = 75;
n1.sigma = 10;
py1 = 1-py0;
%Where to evaluate (and draw)
supNodes = 0:1:100;
g0 = zeros(length(supNodes));
g1 = g0;
% Inline-definition of Gaussian-Function
gauss=inline("1/(sigma*sqrt(2*pi))*exp(-(x-mu)^2/(2*sigma^2))",'mu','sigma','x');
% Evaluate the gaussians
% FIXME: In matlab it might be better to pass a vector instead of using a for-loop.
% But they way I did it, didn't work. Feel free to fix it!
for i=1:length(supNodes)
g0(i) = gauss(n0.mu,n0.sigma,supNodes(i));
g1(i) = gauss(n1.mu,n1.sigma,supNodes(i));
end
% Calculate Probability p(y|x) for every x (in supNodes)
% Priors are not taken into account here
py0x = g0./(g0+g1);
py1x = 1-py0x;
figure()
subplot(2,2,1)
plot(supNodes,g0,'r',supNodes,g1,'b',supNodes,py0x,'r.',supNodes,py1x,'b.');
hold on
plot([55,55],[0,1],'color',[0 0 0],'-'); %Vertical line for navigation
% FIXME: The legend is not properly labeled (the colors are not adjusted...)
title('Red: n0.mu = 35, n0.sigma = 10; Blue: n1.mu = 75, n1.sigma = 10');
legend('r-: y=1','b-: y=2','r.: p(x|y=0)','b.: p(x|y=1)','Location','west');
legend boxoff;
xlabel('x');
ylabel('p(y|x) [no priors taken into account]');
% Calculate logistic Regression with priors p(y0)=p(y1)=0.5
F = exp(-log(py0/py1)-log(py0x./py1x));
logReg=1./(1+F);
subplot(2,2,3)
plot(logReg,'color',[0 .5 0]);
xlabel('x');
ylabel('logisticRegression(x)');
legend('p(y0)=p(y1)=0.5');
% Calculate logistic Regression with priors p(y0)=0.25, p(y1)=0.75
py0=0.25;
py1=1-py0;
F = exp(-log(py0/py1)-log(py0x./py1x));
logReg=1./(1+F);
hold on
plot(logReg,'b');
plot(ones(1,length(supNodes))*0.5,'color',[0 0 0],'-'); % Horizontal line for navigation
plot([55,55],[0,1],'color',[0 0 0],'-'); %Vertical line for navigation
legend('g: p(y0)=p(y1)=0.5','b: p(y0)=0.25, p(y1)=0.75');
legend boxoff;
hold off
%% Do the very same calculations again, but for n0.sigma = 25 now.
% Source-Code is mostly identical to the upper one
%Parameters of Gaussian for class y=0
n0.mu = 35; %mean
n0.sigma = 35; % deviation %% Changed to previous example!
py0 = 0.5; % prior-probability
%Parameters of Gaussian for class y=1
n1.mu = 75;
n1.sigma = 10;
py1 = 1-py0;
%Where to evaluate (and draw)
g0 = zeros(length(supNodes));
g1 = g0;
% Evaluate the gaussians
% FIXME: In matlab it might be better to pass a vector instead of using a for-loop.
% But they way I did it, didn't work. Feel free to fix it!
for i=1:length(supNodes)
g0(i) = gauss(n0.mu,n0.sigma,supNodes(i));
g1(i) = gauss(n1.mu,n1.sigma,supNodes(i));
end
% Calculate Probability p(y|x) for every x (in supNodes)
% Priors are not taken into account here
py0x = g0./(g0+g1);
py1x = 1-py0x;
subplot(2,2,2)
plot(supNodes,g0,'r',supNodes,g1,'b',supNodes,py0x,'r.',supNodes,py1x,'b.');
% FIXME: The legend is not properly labeled (the colors are not adjusted...)
title('Red: n0.mu = 35, n0.sigma = 25; Blue: n1.mu = 75, n1.sigma = 10');
legend('r-: y=1','b-: y=2','r.: p(x|y=0)','b.: p(x|y=1)','Location','west');
legend boxoff;
xlabel('x');
ylabel('p(y|x) [no priors taken into account]');
% Calculate logistic Regression with priors p(y0)=p(y1)=0.5
F = exp(-log(py0/py1)-log(py0x./py1x));
logReg=1./(1+F);
subplot(2,2,4)
plot(logReg,'color',[0 .5 0]);
xlabel('x');
ylabel('logisticRegression(x)');
legend('p(y0)=p(y1)=0.5');
% Calculate logistic Regression with priors p(y0)=0.25, p(y1)=0.75
py0=0.25;
py1=1-py0;
F = exp(-log(py0/py1)-log(py0x./py1x));
logReg=1./(1+F);
hold on
plot(logReg,'b');
legend('g: p(y0)=p(y1)=0.5','b: p(y0)=0.25, p(y1)=0.75');
legend boxoff;
hold off
Zunächst mal Vorsicht, Logistic Regression war nicht gerade mein Lieblingsthema =)
-
Frage: Ja, sollte durch die Mitte gehen. MATLAB-Indizes trolololololol

“plot(Y) creates a 2-D line plot of the data in Y versus the index of each value. If Y is a vector, then the x-axis scale ranges from 1 to length(Y).”
Ergo sind alle Plots in den unteren subplots um 1 nach rechts verschoben, wenn du [m]supNodes[/m] wieder mit angibst, sollte es stimmen. -
Frage: Die Logistische Funktion ist an sich schon streng monoton, aber an der Stelle, wo normalerweise das “x” ist, packst du ja eine Gleichung hin. Und die ist eben nicht (wie x) monoton sondern im Allgemeinen quadratisch bei Gaussian PDFs. Folglich läufst du in der logistischen Funktion irgendwann wieder rückwärts mit entsprechendem Ergebnis.
-
Frage: Ja. Warum die decision boundary so verlaufen muss, ist ja wieder an der Kovarianz erkennbar.
-
Frage: Wenn du mehrere Verteilungen gleichzeitig anschaust, dann hast du ja eine gewichtete Summe der Einzelverteilungen, wobei die nicht-negativen Gewichte genau die Priors der jeweiligen Verteilung sind. Und die müssen sich ja zu 1 summieren. Daraus kann man dann ganz leicht zeigen, dass die Summe unter der ganzen Kurve auch wieder 1 ist. Bei K Klassen:
Wegen dem FIXME, hast du mal elementweise Operatoren ( ./ usw.) in deiner gauss-Definition probiert? Und spricht eigentlich was gegen [m]Y = normpdf(X,mu,sigma)[/m] ? Die sollte das auf jeden Fall können.
Danke schonmal für deine Antwort!
Nochmal zu Frage 4, wie sich priors in einem 1D Plot auswirken, bzw. deine Antwort der Vollständigkeit halber nochmal an meinem Beispiel verdeutlicht
Basierend auf deiner Gleichung in der ersten Zeile lassen sich die pirori-Wahrscheinlichkeiten mit in den Vorfaktor einbauen:
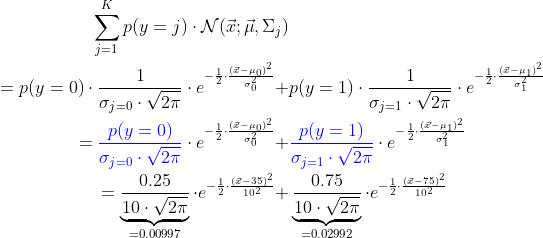
Blau markiert sieht man, wie die priors Teil des Vorfaktors werden, anschließend hab ich dann noch meine Zahlenbeispiele eingesetzt.
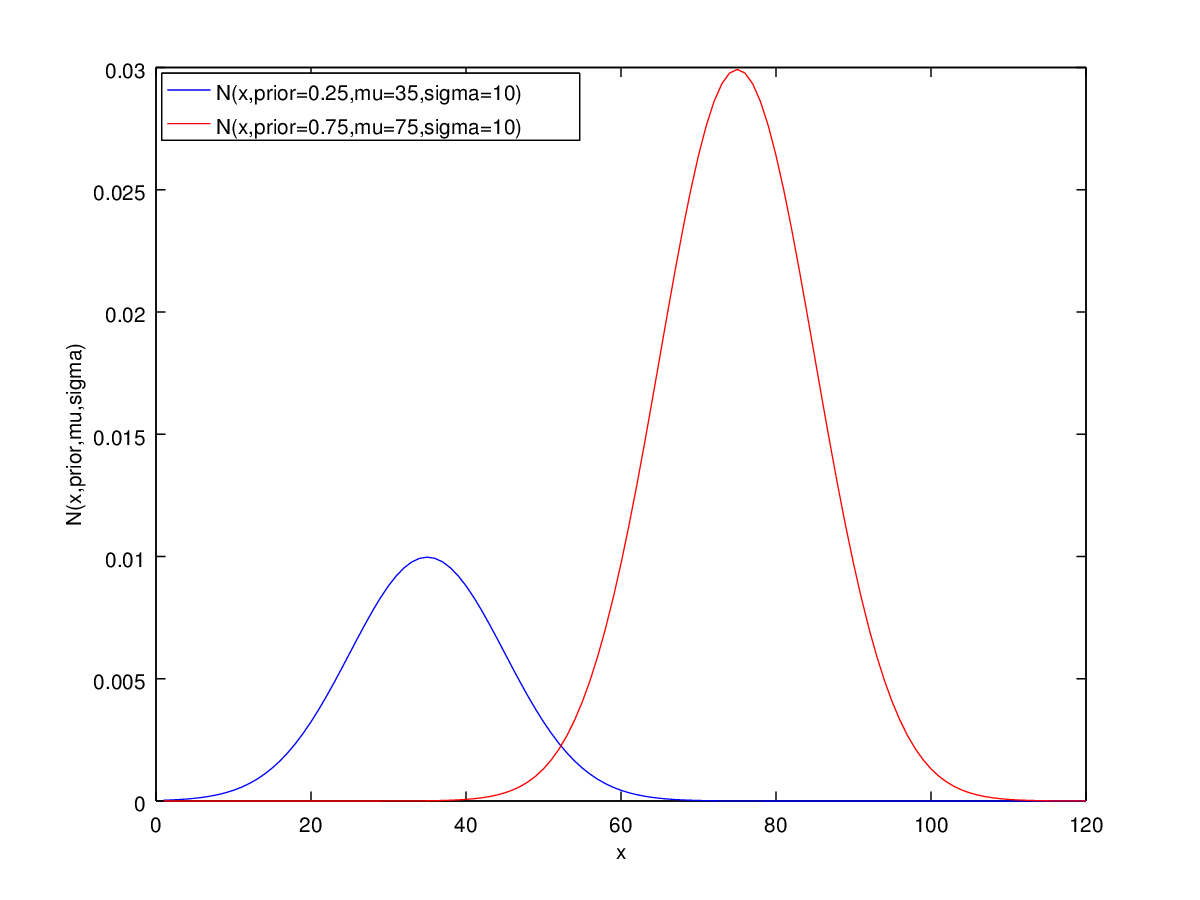
Das lässt sich dann auch in Matlab wieder plotten:
Offensichtlich nimmt der blaue Graph eine kleinere Fläche ein.
Mit trapz hab ich das ganze auch numerisch in Matlab evaluiert:
area0 = 0.24991
area1 = 0.75000
Ratio = 0.33322Also, lässt sich zusammenfassend sagen, dass sich priors auf die Fläche der Kurve auswirken, und alle Kurven addiert die Fläche 1 ergeben müssen.
Hier wieder der zugehörige Matlab-Code:
% Inline-Definition of Gaussian, taken priors into account!
gauss=inline("prior/(sigma*sqrt(2*pi)).*exp(-(x-mu).^2./(2*sigma^2))",'prior','mu','sigma','x');
% Priors:
py0 = 0.25;
py1 = 1 - py0;
% Means:
mu0 = 35;
mu1 = 75;
% Deviations:
sigma0 = 10;
sigma1 = 10;
% Evaluate
supNodes = 1:1:120;
g0 = gauss(py0,mu0,sigma0,supNodes);
g1 = gauss(py1,mu1,sigma1,supNodes);
plot(supNodes,g0,'b',supNodes,g1,'r');
xlabel('x');
ylabel('N(x,prior,mu,sigma)');
legend('N(x,prior=0.25,mu=35,sigma=10)','N(x,prior=0.75,mu=75,sigma=10)','Location','northwest');
area0 = trapz(g0)
area1 = trapz(g1)
Ratio = area0/area1